第一把 AtCoder,可以说是真的菜了,E 题调到死都没调出来...
C - Align
题意
给定 n 个数字,要求排成一排后任意两个数字之差的绝对值之和最大,求最大值
分析
一定是将数列排序后分成两半,前一半和后一半交替排列。绝对值符号可以去掉,然后每个数字计算次数只跟其位置有关,最后分类讨论一下就好了。
1 |
|
D - Crossing
题意
给定 n,问是否存在这样的集合组:
- 1-n 每个数字都恰好被包含在两个集合中
- 任意两个集合仅有一个相同数字
分析
n 条边的完全图
1 |
|
E - Equilateral
题意
给出一张仅含 '#' 和 '*' 的矩阵,问位置三元组的数目,其满足每个位置上的字符都是 '#' 且任意两点的麦哈顿距离相同
分析
跟题解大致相同的思路。
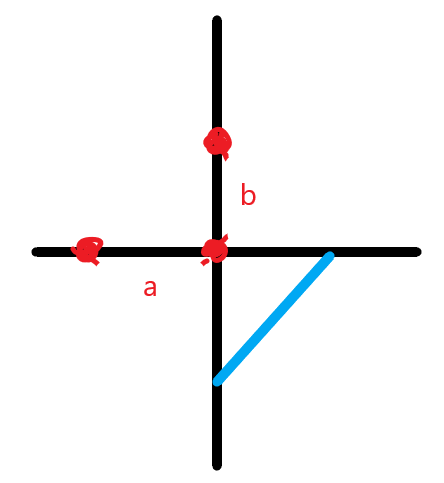
中心红点是三点麦哈顿距离的交点。a 和 b 长度相同,第三个点坐落在蓝线上。故先枚举中间的红点,再枚举另外俩红点的位置,统计蓝线上的点的数目即可。预处理斜线前缀和,复杂度O(n^3)
1 |
|